Arsitektur dan Organisasi Komputer - Computer Arithmetic

ALU -> melakukan kalkulasi dalam komputer.
         -> Handles integers, may handle floating point (real) numbers

Integer Representation
- 0 and 1 merepresentasikan semuanya.
- Contoh: 41 = 00101001
- No minus sign
- Sign Magnitude (pd leftmost bit, 0 utk +, 1 utk - )
- Two's Complement

TWO'S COMPLEMENT
-> negating is fairly easy
cth:
3 = 00000011
boolean complement gives 11111100 (1 jd 0, 0 jd 1)
add 1 to LSB (Least Significant Digit -> digit plg blkg) gives 11111101 -> -3

-> range of numbers:
8 bit two's complement: 2^7 -1 to -2^7
16 bit two's complement: 2^15 -1 to -2^15

-> addition and subtraction
addition: normal binary addition
subtraction: e.g. a - b = a + (-b)

-> multiplication
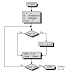
a) Unsigned Binary Multiplication

Execution Example:
Keterangan:
C = Carry
A = tempat utk menampung perhitungan
Q = pengali (multiplier)
M = yang dikali (multiplicand)

Penjelasan:
Dari algoritma (flowchart) diatas, kita aplikasikan buat melakukan perkalian bilangan positif. Awalnya, nilai carry (C) dan A di set 0. Kita akan mengalikan 13 dengan 11 (1101 dan 1011). Count bernilai n, yaitu jumlah digit Q.
Next, kita lihat apakah Q0 nya bernilai 1? Q0 adalah LSD dari Q. Karena awalnya Q0 bernilai 1, kita menambahkan (add) A+M dan shift 1 digit ke kanan kanan. Jangan lupa count-1, nilai count sekarang adalah 3. nilai count != 0, maka diulang kembali.
Selanjutnya, nilai Q0 berubah menjadi 0, sehingga kita lakukan shift kembali dan count = 3-1 = 2. Nilai count != 0, maka perulangan kembali dilakukan.
Lalu, setelah di shift nilai Q0 menjadi 1, sehingga A+M menjadi 1101, dan shift kembali dilakukan. Count sekarang bernilai 1, dan belum sama dengan 0, sehingga perulangan lagi.
Akhirnya, kita lihat bahwa nilai Q0 adalah 1, sehingga A+M, Shift dan Count sekarang == 0, sehingga proses berakhir.

Hasil akhir dari perkalian adalah A, Q sehingga = 10001111 atau 143.

b) Signed Binary Multiplication -> menggunakan Booth's Algorithm

Contoh:

Penjelasan:
Rata" sama kyk unsigned binary sih, tapi bedanya yang ini ada Q-1 nya. Ikutin flowchart aja ya wkwk :p

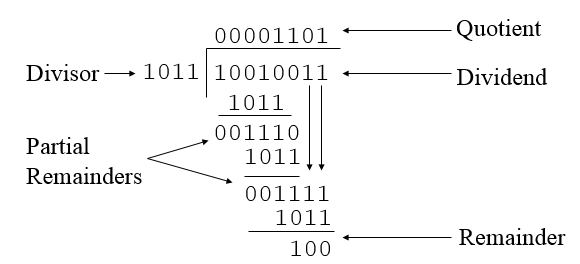
-> division:
a) Unsigned Binary Division
    - Cara pembagian biasa:

    - Umumnya dibagi menjadi 2: restoring dan non-restoring
1) Restoring
cth: 8/3 -> 1000 / 11

2) Non-restoring
cth: 8/3 -> 1000 / 11

Semoga dgn membaca sendiri udah bisa ngerti ya :) kalo emang masih blm ngerti feel free to ask :)

REAL NUMBERS
-> numbers with fraction
-> floating point:

1) Single precision/format

2) Double Precision Format

Cara menghitung biased exponent

dan seterusnya.

Cara menghitung floating point:
contoh:
a. FP dari 102?
1) Cari biner dari 102 -> 1100110

2) Ubah bentuknya menjadi 1,...
1100110 -> 1,100110 x 2^6 (karena komanya geser 6 biner)

3) Cari biased exponentnya
Bias: 127
geser 6 biner -> E = 6
Bias + E = 133
Biner dari 133 = 10000101

4) Masukkan ke bentuk Floating point
 0    10000101   10011000000000
(+)    (Biased)     (Dapet dari angka dibelakang koma)

b. konversi hexa ke desimal dalam bentuk floating point (gw gapunya term yg lebih bagus dr ini lol)
cth: 8 3 6 0 0 0 0 0
1) ubah ke bentuk biner
1000 0011 0110 0000 0000 0000 0000 0000

2) ubah ke bentuk floating point
   1      | 000 0011 0 |  110 0000 0000 0000 0000 0000

(sign)    (biased)        (fractions)

3) ubah ke desimal, caranya:

-> sign = 1 berarti minus (-)

-> biased = 6, utk mjd 127 berarti kurang 121 -> 2^(-121)

-> fractions = pake cara angka dibelakang koma, sehingga 0,5 + 0,25 = 0,75

-> lalu, gabungin semuanya~

    - 1,75 x 2^(-121)

(jangan lupa didpn koma tambahin 1)

Hope it helps!