Ax = b
Matrix transformasi A akan mengubah vektor x menjadi vektor b.
cth:
2 -4 -8
3 -6 2 = -12
1 -2 3 -4
(^^^ceritanya matrix ya)
Ukuran A = m x n, dengan menyelesaikan Ax = b artinya akan mencari vektor x kedalam ruang vektor n yang mentransformasikan vektor b melalui vektor R^m
Matriks Transformasi
Transformasi T dari R^n ke R^m adalah aturan yang assign each other
T: R^n -> R^m
R^n = domain dari T
R^m = kodomain dari T
T(x) dalam R^m adalah image dari x dalam transformasi T.
Kumpulan dari image disebut dengan Range.
Cth:
A = 1 0
2 1
0 1
x = 2
1
Tentukan transformasi T:R^2 -> R^3 (Ruang 3dimensi)
by T(x) = A(x)
Jawab:
1 0 2
2 1 x 2 = 5
0 1 1 1
Transformasi Linear
dikatakan linear jika memenuhi hal ini:
(additive property)
(homogency property)
T(0) = 0 dan T(cu + dv) = c T(u) + d T(v)
Contoh:
T:R^2 -> R^3 mentransformasi yang memetakan e1 ke y1 dan e2 ke y2. Tentukan image dari:
[3]
[2]
dan
[x1]
[x2]
Jawab:
Matrix Transformasi:
A = ( T(e1) | T(e2) | ... | T(en) )
A ( T(e1) | T(e2) ) = ( y1 | y2 )
Contoh Soal 2:
Transformasi T:R^3 -> R^2
T(x1, x2, x3) = ( | x1+x2 |, 2+5x2 )
Buktikan bahwa transformasi tidak linier!
Jawab:
Persamaan diatas tidak sesuai dengan T(0) = 0 ataupun T(cu) = c T(u).
Proof =
T:v -> w adalah linear transformation dimana vektor v memiliki dimensi terbatas. Jika S = {v1, v2, v3} adalah basis dari v, maka image dari vektor v dalam V dapat ditulis:
Lat. soal: halaman 465


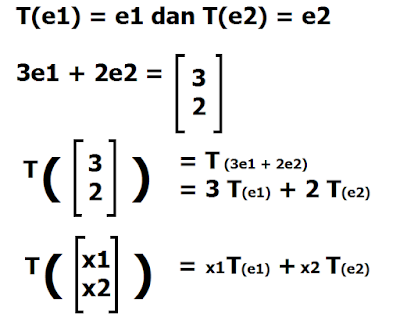








0 comments:
Post a Comment