Ringkasan Aljabar Linear - Materi UTS (Part 1)

CHAPTER 1
Linear Sytems:
1) No Solution, contoh:
    x+y = 4
    3x+3y = 6
    dengan menggunakan eliminasi:
    3x+3y = 12
    3x+3y = 6   -
    ----------------
     0      =  6 (invalid)

2) One solution, contoh: x=4

3) Infinitely many solutions, contoh:
    4x - 2y = 1
    x = 1/4 +1/2 y
    sehingga nilai x bergantung pada nilai y. bila nilai y=2, x bernilai 5/4.

Penyelesaian persamaan linear menggunakan matrix
 

Reduced Row-Echelon Form

Syarat:
1) Memiliki nilai 1 utama (leading one) pada setiap baris yang isinya bukan hanya nol. Leading 1 dilihat dari angka 1 di posisi paling kiri.
2) Leading 1 di baris berikutnya berada diposisi lebih kanan daripada atasnya
3) 1 kolom yang memiliki leading 1 terdiri dari angka 0 kecuali leading 1 itu sendiri.

Contoh konversi matrix dalam bentuk row-echelon ke persamaan linear:

dalam contoh (a), pada baris ketiga dapat dilihat persamaan linear berupa 0x+0y+0z = 1, dimana tidak mungkin terjadi. Oleh sebab itu contoh (a) tidak dapat diselesaikan
pada contoh (b), persamaan linear yang didapat adalah
   x+3z = -1
   y-4z = 2
karena x dan y merupakan satu utama, maka bentuknya diubah menjadi:
   x = -1-3z
   y = 2+4z
variabel z dapat di misalkan sebagai t, sehingga:
   x = -1-3t
   y = 2+4t
   z = t
pada contoh (c), persamaan linearnya adalah x-5y+z = 4
seperti contoh (b), x merupakan satu utama sehingga
   x = 4+5y-z
dimana y dan z merupakan variabel bebas sehingga dapat dimisalkan
   x = 4+5s-t
   y = s
   z = t

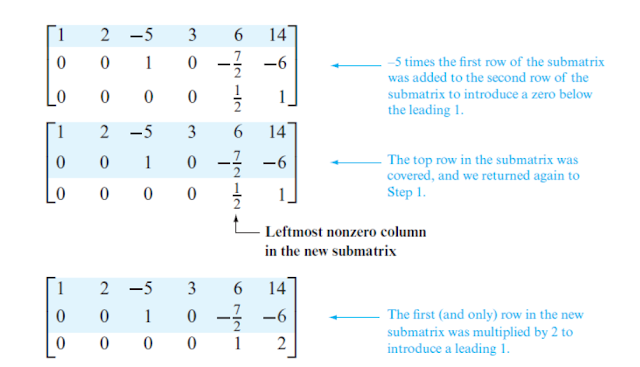
eliminasi matrix untuk mendapatkan bentuk reduced row-echelon:

eliminasi untuk menemukan bentuk reduced row-echelon form diatas dapat disebut juga dengan Eliminasi Gauss-Jordan. Eliminasi ini terdiri dari 2 bagian, yaitu forward phase yang mencari nilai nol dibawah leading 1 dan backward phase yang mencari nilai 0 diatas leading 1. Eliminasi Gauss hanya mencari sampai step 5 pada contoh diatas (row-echelon form)

Latihan:

(jawaban dan pembahasan dapat dilihat di ebook halaman 16)

Sistem Persamaan Linear Homogen:

pada sistem persamaan linear homogen terdapat 2 solusi:
1) solusi trivial (dapat di invers), nilai variabel adalah 0. contoh: ax + by = 0
2) solusi non-trivial, nilai sebuah variabel akan memengaruhi nilai variabel lain. contoh: x1 = x2 - 2x3

 cara menyelesaikan sistem persamaan linear (dengan subtitusi biasa):

Matrix
1) penjumlahan matrix dengan ekspansi kolom-baris:

2) Transpose matrix

3) Trace -> penjumlahan diagonal utama sebuah matrix square

4) Invers matrix

    Penyelesaian persamaan linear dengan invers matrix:

    Hubungan invers dan transpose:

    Matrix elementer (Elementary Matrix)

Mencari invers dengan matrix elementer:

Mencari invers matrix dengan operasi baris:

Aplikasi persamaan linear matrix
1) Network system

2) Traffic

 3) Circuit

CHAPTER 2 - DETERMINAN
Mencari determinan dengan ekspansi kofaktor:

cara lain mencari determinan (cara SMA)

Mencari determinan dengan reduksi baris:

Mencari determinan dengan gabungan reduksi baris dan ekspansi kofaktor:

Sementara segini dulu, untuk chapter selanjutnya akan di update lagi di post baru.
Latihan soal dapat dilihat di ebook.
Ebook: Howard Anton, Elementary Linear Algebra, 11th Ed.